本文转自: https://blog.si-on.top/2024/note4camera/
仅做个人收藏,版权归原作者所有
到底认识达到何等程度才能冠以了解之名呢?
——秉
✍文章痕迹
写作时间线
2024-07-08
- 为摆脱过于学生气的摄影风格,革新自己追求更专业的摄影,决定购买专业设备
- 分析2024年各相机厂商主流产品价位与配置
- 发觉知识之欠缺,开始补习相机设备层面的相关知识
2024-07-09
- 阅读人民邮电出版社2021年出版的『图解数码相机原理和结构』,形成文章主体内容与主题——非原创笔记
- 开始搜罗大量资料
2024-07-10
- 阅读文献『浅析单反拍摄中的光圈衍射现象』,添加了对星芒现象的笔记,并启发思考了人眼瞳孔的形状与光芒的关系——天下没有无芒的光。
- 夜班开始正式撰写此文
2024-07-14
- 摄影教材《摄影技艺教程(第七版)》
- 学习了镜头的结构
- 添加等效焦距部分内容
2024-07-18到7-30
- 完善文章
- 完善公式
- 调整文章结构并发布
注意:本文所关注的设备为『单反相机』与『微单相机』等常见的可以更换镜头的摄影装置,部分笔记如镜头、光圈、防抖可能对手机镜头、卡片相机、显微镜等光学装置具有普适经验。
序:欢迎来到黑箱时代
大抵是因为这个时期人们太懒了很看中便捷性,二十一世纪一二十年代生产的消费电子产品都做成了黑箱型——简单到近乎幼稚的交互下裹藏着难以理解的复杂。从服务器中的Docker到日趋同质化的智能手机,再到计算机科学中的神经网络,乃至大语言模型,无一不可看作是一个黑箱。
简单、优雅、便捷背后的代价是沉重的。这样的设备/程序一但出现了故障,难以理解的复杂性足以把任何维修的热情扑灭。人们只能重启、格式化,祈祷它自行修复。意外事故背后,除了一遍遍地证明自己的愚不可及外,无论怎样复盘,人们总一无所获。上个月我曾经尝试用Docker部署火鱼(FireFish,类似于Mastodon),构建出现了故障,但镜像是打包好的,简直没法修复——修复后升级又是个问题,最后还是从头构建、一步步安装依赖才成功部署。
不论怎样完美的东西,只要有人支持,必定会有人反对,不论出于何种目的。
黑箱化是一种大趋势,象征着机器的人化,那么反黑箱化就是与之相伴而生的逆流——让机器重新回到可认识、可拆卸、可修复的机器的疆域。反黑箱化——是黑箱时代发烧友拥有的最后一份倔强。他们高喊着『拆开黑箱!打开魔盒!让人类再次拥有制造工具的能力!』
说来惭愧,我的第一个相机是2021年买的索尼DSC-WX350,这是台傻瓜卡片机,一种典型的黑箱型设备——不可更换镜头、不可拆卸机身,操作简单,能力强悍憨。2023年,一次冒雨拍摄割麦机抢收场景后,镜头进水,水干后留下了污渍,想尽各种办法也没能清理掉。而后忍无可忍,参照国外大佬的拆机视频冒险拆机,然而灰没清掉,机身装不回去了(准确的说是装上了但开不卡机),最后送修,画了两百块啪啪打脸。
维修失败之后,我得到了什么呢?除了证明自己又多么愚蠢,科技产品是多么复杂之外,我一无所获。
人永远一无所获——这是黑箱化带来的必然结果。你以为会个Docker指令就成运维了?你以为跟GPT对话两轮就成为专家了?你以为照猫就能画虎了?走路只能一步一个脚印,直接飞去终点的都是云玩家。
知识需要掰开揉碎、需要细嚼慢咽,任何形式的取巧都是给自己挖坑。我对摄影有兴趣,但始终停留在兴趣层面,不舍得投入,只关注表面文章(比如构图、后期、色调了),几年来已经挖了不少坑了,今天就趁此机会,把摄影从头好好理理。此外,为了增加写作积极性,文章一旦完善好,就分期给自己买一台可换镜头的真相机+一大堆镜头,嘻嘻嘻嘻嘻嘻。
镜头篇
相机简单可以拆分为机身与镜头,镜头直接影响成像效果,这也是可更换镜头相机的魅力所在。
此部分内容大多为《摄影技艺教程(第七版)》的笔记。
如何评测一个镜头:透镜特点与像差解读
现代相机的镜头大多很复杂,特别是那些光圈大的、可变焦的,为了消除畸变、像差,都使用了很多组透镜。
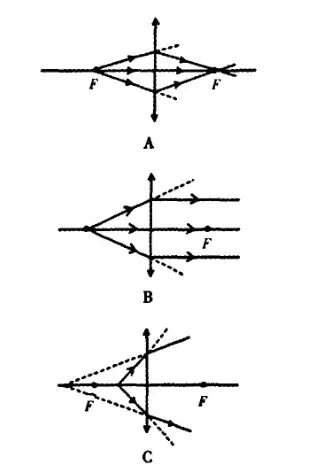
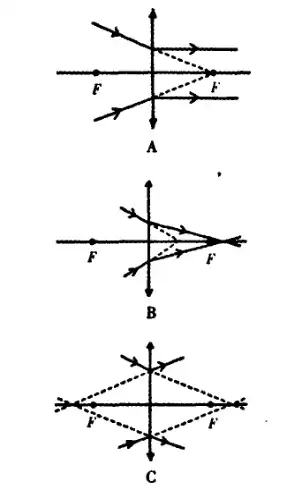
透镜可以按照折射率的不同,可以分为两种——凸透镜与凹透镜,其特点[1]如下:
| 凸透镜 | 凹透镜 |
|---|---|
| 汇聚光线 | 发散光线 |
| 反射光为实像 | 反射光为虚像 |
 |
 |
| “双凸透镜”、“平凸透镜”、“凹凸透镜” | “双凹透镜”、“平凹透镜”、“凸凹透镜” |
两者的作用也各不相同(不考虑畸变修复)。凸透镜是把外界的光线(自然光可近似看作平行光)汇聚到焦点上,但在一个无穷小点上的像是无法被捕获的,而凹透镜是把汇聚的光线进行发散,使光线最会达到传感器/目镜/取景框的时候拥有合适的大小。
理论上讲,两者适当组合起来就还可以成像,但现代相机上一般不是简单的凸透镜与凹透镜组合,因为在21世纪,光学透镜都做不到特别精密,这就会导致像差。像差基本可以分为以下六种:
| 像差 | 原理图 | 特点 | 修复措施 |
|---|---|---|---|
| 球差 | 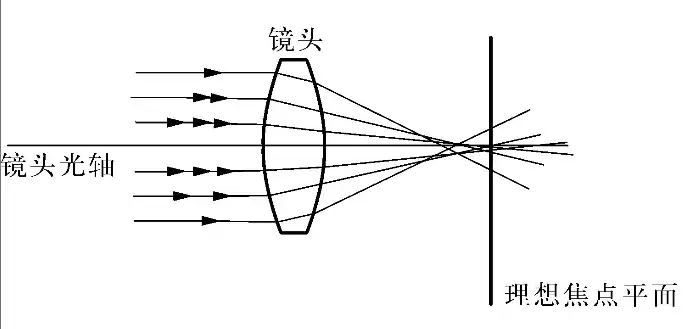 |
光通过球面透镜后,因折射情况不同而不能聚焦于同一焦点的现象 | 采用非球面透镜[2];增加N片透镜,凹凸相抵;缩小光圈(只利用透镜的中间部分) |
| 色差 | 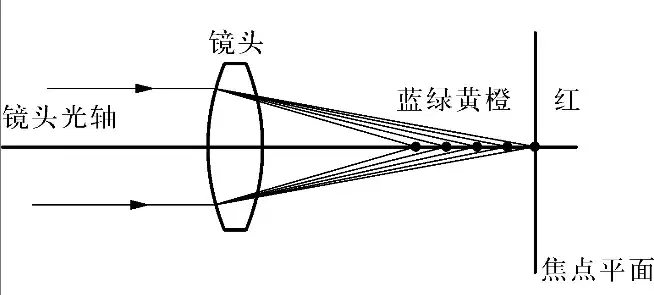 |
镜头对不同色光产生的聚焦点不一的现象 | 采用多片透镜凹凸相抵;镀膜;特殊光学材料 |
| 畸变 | 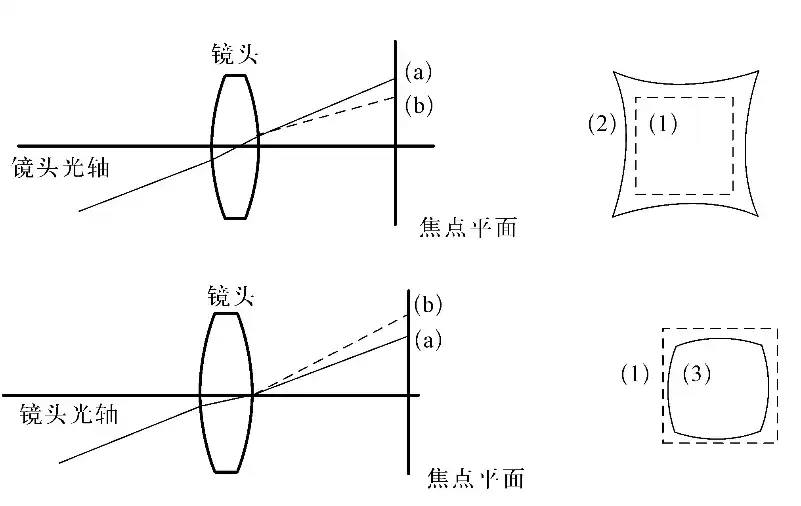 |
透镜成像时,视场的不同区域所形成的影像放大率不同而产生的一种变形(小于10%就不影响) | 采用对称结构的镜头 |
| 像散 | 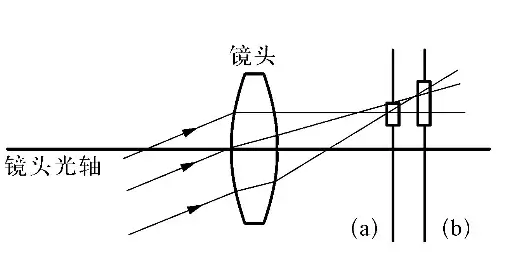 |
影响像场边缘部分的影像清晰度,使镜头主光轴外的光线通过镜头成像时,不能聚焦于同一平面。(相对来说,镜头焦距越短,像散现象就越严重) | 缩小光圈 |
| 场曲 | 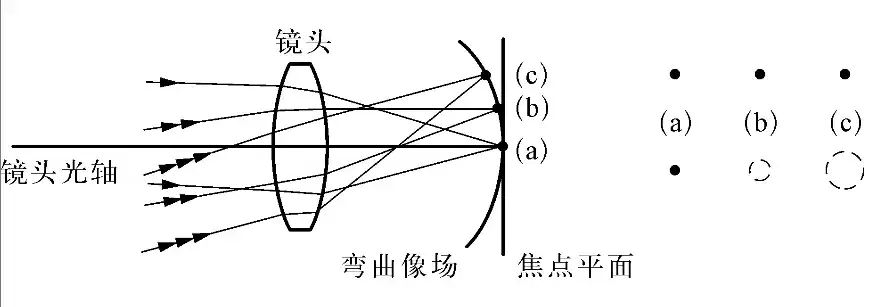 |
平面物体通过镜头成像时,不能在焦平面清晰地结像,而是在一个盘形曲面上清晰结像。存在场曲的镜头,当向平面物体中央聚焦时,画面四周成像清晰度下降;当向平面物体边缘聚焦时,画面中央成像清晰度下降, | 缩小光圈 |
| 彗差 | 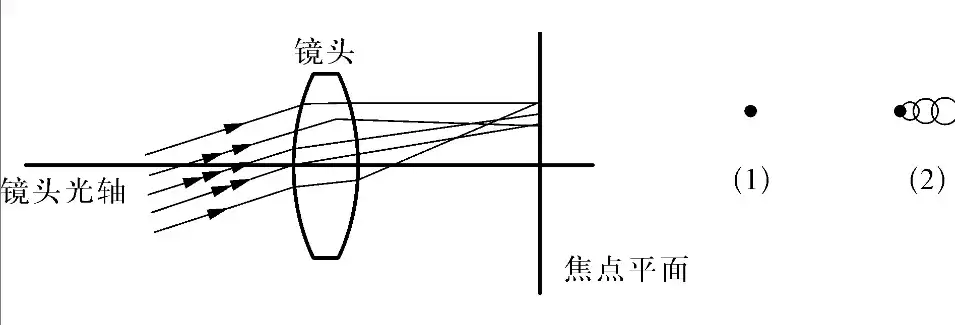 |
透镜光轴外的光线(即斜射光线)在成像时不能在像平面聚焦于一点,而是形成彗星状(梨状)的弥散斑构成影像 | 缩小光圈;采用对称结构的镜头设计 |
除此之外,还有一种变形——透视变形(近大远小),这是自然界的基本规律[3],可以用移轴镜头进行消除。
温馨提示:减小像差的基本操作是减小光圈,然而减小光圈又容易因为衍射效应导致锐度降低,所以这也是个双难选择。
温馨提示的温馨提示:增加锐度除了换镜头外也可以通过算法来实现。
数码相机主要由机身和镜头组成,机身的核心就是CMOS/CCD感光元件,可以类比人眼。而镜头焦距的含义,对定焦镜头来说,一般可以理解为“镜头中心至胶片平面的距离”。
| 数码相机 | 人 |
|---|---|
| 镜头 | 眼球 |
| 感光元件 | 视网膜 |
镜头的参数、特性有很多:这里挑几个核心的进行讨论
焦距与视角
为了更好理解,我们用一种更为直观的方法来理解视角与焦距——窗户模型。
首先,我们定义
- 人眼的视野[4]为60°(θ0=60∘\theta_0=60^{\circ}θ0=60∘)
- 你身处在一个很长的室内走廊里
- 走廊尽头有一个半径1m的圆形窗户(r0=1r_0=1r0=1)
- 窗外有5米处有一棵高6m的树(l′=5,h=6l^{‘}=5,h=6l′=5,h=6)
- 圆心、树的中心(3m处)、你的眼睛三者在一条直线上
- 你的视力很好,外面光照充足,屋内没有其他光源干扰
- 视角表示你能看到的景物,用θ\thetaθ表示;眼睛与窗户的距离为lll;观察到的实际视野半径用rrr表示
周边视觉的解读
This is vision outside of the range of stereoscopic vision. It can be conceived as bounded at the center by a circle 60° in radius or 120° in diameter, centered around the fixation point, i.e., the point at which one’s gaze is directed. However, in common usage, peripheral vision may also refer to the area outside a circle 30° in radius or 60° in diameter.
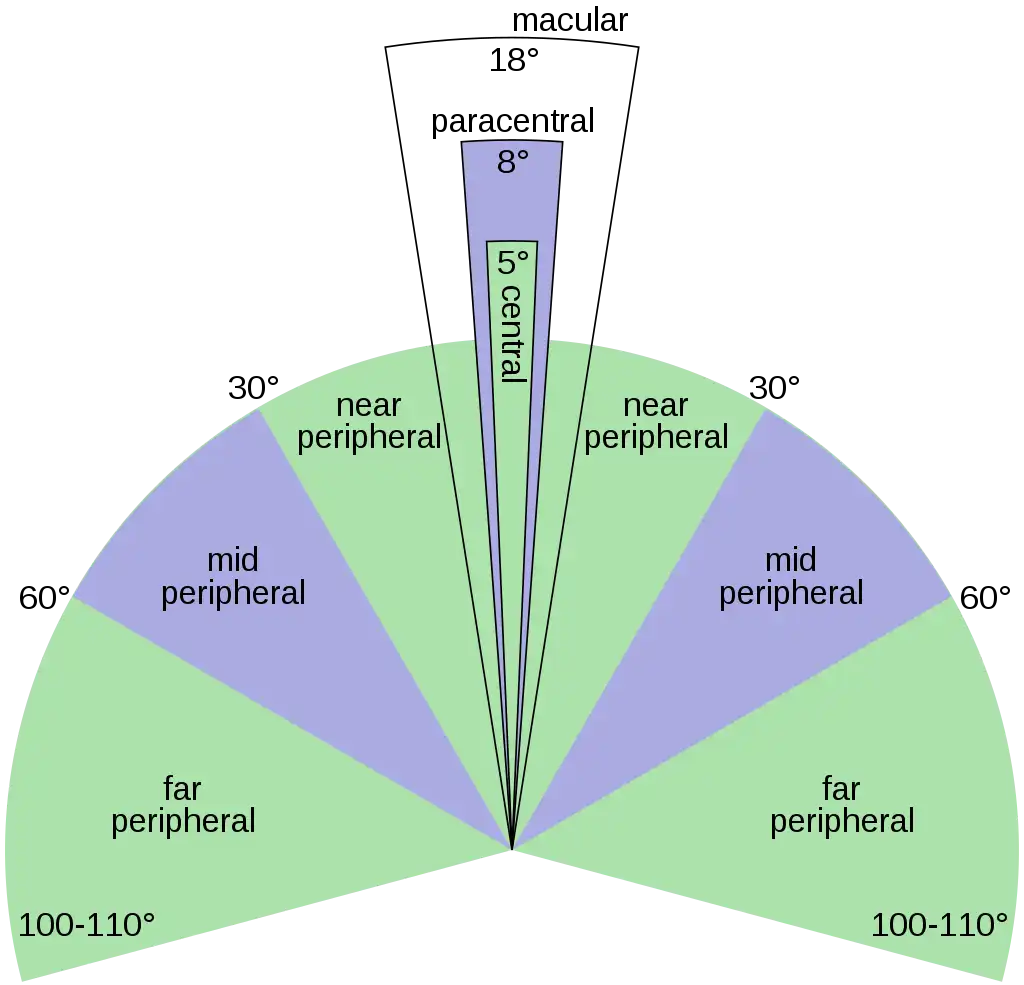
那么,当你站在
- 【无限长焦】走廊另一边的极远处(l=∞l=\inftyl=∞),你会看到一个亮点,这时候视角可近似看作0∘0^{\circ}0∘
tanθ0=r0l=1∞≈0⟹θ=0∘\tan\theta_0=\frac{r_0}{l}=\frac{1}{\infty}\approx0\Longrightarrow \theta=0^{\circ}tanθ0=lr0=∞1≈0⟹θ=0∘
- 【超长焦】站在距离窗户10m处,你会看到树木中心实际距离1.5m半径内的景物,视角约为11.4∘11.4^{\circ}11.4∘
tanθ1=rl=110=0.1⟹θ1=5.71∘\tan\theta_1=\frac{r}{l}=\frac{1}{10}=0.1\Longrightarrow \theta_1=5.71^{\circ}tanθ1=lr=101=0.1⟹θ1=5.71∘
r1=(l′+l)×r0l=(5+10)×110=1.5(m)r_1=\frac{(l^{‘}+l)\times r_0}{l}=\frac{(5+10)\times1}{10}=1.5(m)r1=l(l′+l)×r0=10(5+10)×1=1.5(m)
- 【标准视角】站在距离窗户1.71m处,你的视野中所能清晰看到的景物与没有窗户、墙壁的情况下是一样的,视角为60∘60^{\circ}60∘,可以看到距离树木中心3.886m半径内的景物。
tanθ2=rl=13=0.577⟹θ2=30∘\tan\theta_2=\frac{r}{l}=\frac{1}{\sqrt{3}}=0.577\Longrightarrow \theta_2=30^{\circ}tanθ2=lr=31=0.577⟹θ2=30∘
r2=(l′+l)×r0l=(5+3)×13=3.886(m)r_2=\frac{(l^{‘}+l)\times r_0}{l}=\frac{(5+\sqrt{3})\times1}{\sqrt{3}}=3.886(m)r2=l(l′+l)×r0=3(5+3)×1=3.886(m)
- 【广角】理论上来讲,人眼视角极限是120∘120^{\circ}120∘,当你处于【标准视角】的位置后,不论再怎样接近视角都是不变的,只不过随着距离的接近,景物越来越大(如图中锥形视野)。但是如果把眼睛看作一个超级眼睛——脱离了生理极限——可以无限拓展视野,那么我们就可以得到更大的视野,如图上的蓝色与紫色小人,就得到了126∘126^{\circ}126∘与接近180∘180^{\circ}180∘的视角
上述模型中,窗户可以比作光圈(固定大小)、人与窗户的距离可以比作焦距。我们可以得到如下规律:
- 焦距与视角成反比——焦距长,视角小;焦距短,视角大。视角小意味着能远距离摄取较大的影像比率;视角大能近距离摄取范围较广的景物。
镜头的分类
通过与标准视角的比较,我们可以把镜头分为三种
- 广角镜头——视角大、景深大、纵深感(透视感)强
- 标准镜头——与人眼视角接近,其焦距长度接近相机画幅对角线长度的镜头。摄取景物的范围、前后景物的大小比例带来的透视感等,都与人眼观看效果类同,画面影像显得较真切、自然
- 长焦镜头——视角小、景深小、纵深弱
通过变焦与否,我们又可以把镜头分为定焦镜头与变焦镜头。顾名思义:“在一只镜头上,焦距固定,不能变化的,称为定焦镜头;而焦距有一定变化范围的就称为变焦镜头。”变焦镜头的焦距可在较大的幅度内自由调节,这就意味着在你用一个镜头就可以拍出来广角/标准/长焦的效果!当然变焦的范围越大并非越好,越大就意味着“体积相对较大、像质相对略低、光圈相对较小”,常见的变焦范围如下
- 17~35mm的超广角变焦镜头
- 35~70mm的标准变焦镜头
- 70~210mm的中远变焦镜头
- 200~400mm的远摄变焦镜头
- 28~135mm五倍广角中焦变焦镜头
- 28~300 mm十倍广角至长焦
比如我手里的索尼卡片机,它的焦距范围是4.3~86mm(变焦倍数为20x)就属于广角至长焦范围内的。一般来说,在其他条件不变的情况下,根据照度第一定律:随着距离(焦距)变长,最后抵达被照明物体(CMOS)的光量是会随距离平方递减的,这就会导致最后的照片比较暗淡。因而一个优质/昂贵的变焦镜头的特点便是——恒定大光圈,超大变焦范围、极小畸变。
E=IR2\begin{equation}E=\frac{I} {R^2}\end{equation}E=R2I
(公式中:E为照度(光照强度:illumination);R为对象到光源的距离;I为光源的发光强度(Luminous intensity)。)
根据光圈的定义F=frF=\frac{f}{r}F=rf,恒定光圈意味着随着焦距的变大、光孔直径也会变大。但其工艺复杂,一般的变焦镜头是做不到的,这就导致恒定大光圈的镜头比较贵(当然也可能是另一种噱头)。
此外还有一些特殊的镜头如:
- 微距(Macro)镜头——类似于显微镜,由两个凸透镜组成,可以将物体放大很多倍
- 透视/移轴镜头——用于调整影像透视效果或景深效果的特殊镜头(可以去除透视变形)
- 柔焦镜头——产生虚化
等效焦距
这一部分是三大迷糊(等效焦距、景深、选购)中最为迷糊的部分,在研读了诸多专业/非专业人士写的文章后,终于搞清楚了等效焦距的含义,其中特别感谢赵小麟(1953-)老先生撰写的文章[5],概念解释透彻至极!
等效焦距本身并不难理解,因为它代表的属性很简单而且直观——视角。
镜头的视角是由相机的画幅面积和镜头的焦距两项因素结合形成的。使用传统相机,由于相机的画幅面积是统一的,因此人们就习惯用镜头的焦距来表示镜头的视角。在上文的窗户模型中,我已经提到人眼的视角是60∘60^{\circ}60∘,以此为界限便可以分出广角长焦镜头的视角。
在数码相机时代,由于不同品牌、不同机型的感光元件的面积各不相同,在手机上的CMOS已经达到了11.7″\frac{1}{1.7^{“}}1.7“1之小[6]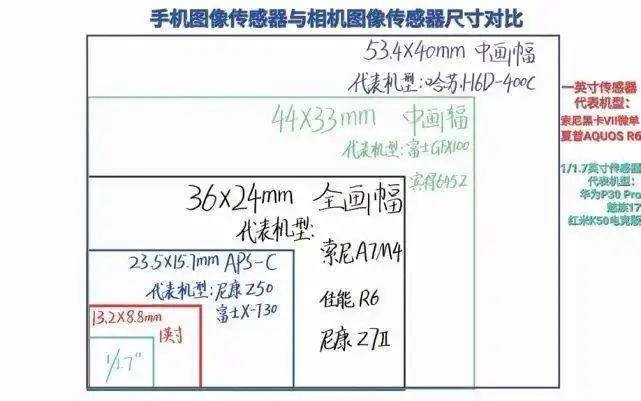
即便是使用相同焦距的镜头,在相同的距离拍摄同一景物,拍摄照片的取景范围却随着画幅的面积变化而有所不同。取景范围不同也就是镜头的视角不同。为了使不同的画幅面积能有一个统一表示镜头视角的标准,依循人们用焦距表示镜头视角的习惯,参照传统 135相机的画幅标准,数码相机中就出现了焦距转换系数与135等效焦距2个概念。
焦距转换系数是数码相机感光元件的画幅面积,与传统 135相机的画幅面积,获得相同的镜头视角时,所需要的2个不同镜头焦距的比值,简言之就是CMOS对角线的比值。两者的对应关系很简单:
等效焦距=实际焦距×焦距转换系数\text{等效焦距}=\text{实际焦距}\times\text{焦距转换系数}等效焦距=实际焦距×焦距转换系数
以我红米手机为例,其主摄的传感器尺寸为1/1.52″英寸[7],亦即对角线长度[8]为:0.65英寸,而全画幅的对角线长度约为2.7英寸,那么其焦距转换系数k=2.70.65=4.15k=\frac{2.7}{0.65}=4.15k=0.652.7=4.15所以等效焦距是实际焦距再乘以4.15。
镜头视角的表示标准是由焦距、视角与画幅面积的互动关系结合形成的。三者的关系如下
-
如果底片尺寸(即画幅面积)已固定,则视角大小完全决定于焦距的长短。焦距越长,视角越小;焦距越短,视角越大;视角与焦距成反比关系。
-
如果镜头的焦距已固定,画幅的大小与镜头的视角成正比。画幅越大,视角越大;画幅越小,视角也越小。
-
如果镜头的视角已固定,镜头的焦距与画幅的 面积也成正比。镜头的焦距越长,画幅的面积越大;镜头的焦距越短,画幅的面积也越小。
景深
景深是指被摄景物中能产生较为清晰影像的最近点至最远点的距离。一般来讲,景深的目的是营造一种主体清晰,前景或背景模糊的虚化效果。
镜头聚焦于被摄景物的某一点,该点在胶片上便产生焦点,焦点是构成影像的最小光点。这种最小光点实际上是一种极小的圆圈(简称像斑),可测量其直径。离开聚焦点前、后的其他景物在胶片上就不能产生焦点,它们的焦点或落在焦平面前面(比聚焦点远的景物)或落在焦平面后面(比聚焦点近的景物),而在胶片上成像的圆圈(光点)都比焦点上的圆圈(光点)增大了。离开聚焦点距离越大的景物(包括离镜头比聚焦点更远或更近),在胶片上结像的圆圈(光点)也越大。
景深公式的推导
此部分内容是下面两篇论文的笔记摘要。
由光学知识可知,垂直于镜头光轴可作很多个平面,位于镜头物方的平面叫物平面,位于镜头像方的平面叫像平面。物平面到镜头中心的距离叫物距uuu,像平面到镜头中心的距离叫像距vvv。现代相机的镜头虽然由很多组镜片组成,其本质仍然可以看作是一块凸透镜,其焦距一般用fff表示。那么根据凸透镜成像规律,有:
1u+1v=1f\begin{equation}\frac{1}{u}+\frac{1}{v}=\frac{1}{f} \end{equation}u1+v1=f1
对于焦距不变的镜头来说,即使像差校正的很彻底,也只能在一对共轭的平面内保证物和像的一一对应关系,使点物成点像。但世界不是二维的,物体大部分是有体积的,这便导致不可能把一个物体的各个部分都准确地对焦,但实际上,照相机确实能够对立体物成平面像。其原因就在于作为观察影像的仪器—— 人的眼睛,其分辨能力是有限的。由光的衍射理论可知,眼睛的最小分辨距离yyy为:
Δy=0.61sλR=0.61观察近距离×光的波长瞳孔直径\Delta y=0.61\frac{s\lambda}{R}=0.61\frac{\text{观察近距离}\times\text{光的波长}}{\text{瞳孔直径}}Δy=0.61Rsλ=0.61瞳孔直径观察近距离×光的波长
由关于最小分辨距离的瑞利判据:当两个斑点中心的间距不小于一个斑点的直径时,人眼是可以区分这两个斑点的。所以,当一个物点所成的像斑斑点的直径ddd不大于眼睛的最小分辨距离时人眼认为像是非常清晰的。即对眼睛而言,相机能成非常清晰的像的,条件就是:d≤Δyd\le \Delta yd≤Δy。一般情况下,相片上允许的斑点(又称为模糊圈)直径可取为d=0.25mmd=0.25mmd=0.25mm或d=0.05mmd=0.05mmd=0.05mm。也就是说,焦平面可在准确焦点前后的一定幅度移动,焦点沿着镜头光轴所允许移动的距离成为焦深(在此不做讨论)
下面来计算下景深,以下图为例。
我们把后面的山看作A,中间的树木看作B,前面的草地看作C,其发出的光线经镜头折射后会汇聚于A′A^{‘}A′、B′、B^{‘}、B′、C′C^{‘}C′点,再记前景深即C点景深为u近=uCu_{\text{近}} = u_Cu近=uC 后景深为u远=uAu_{\text{远}}=u_Au远=uA: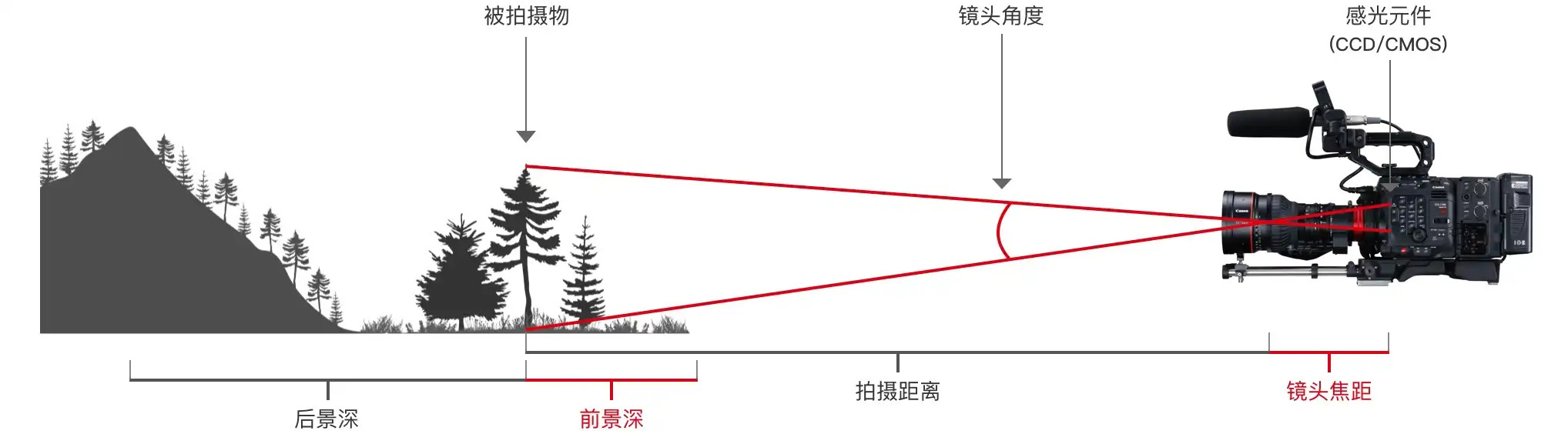
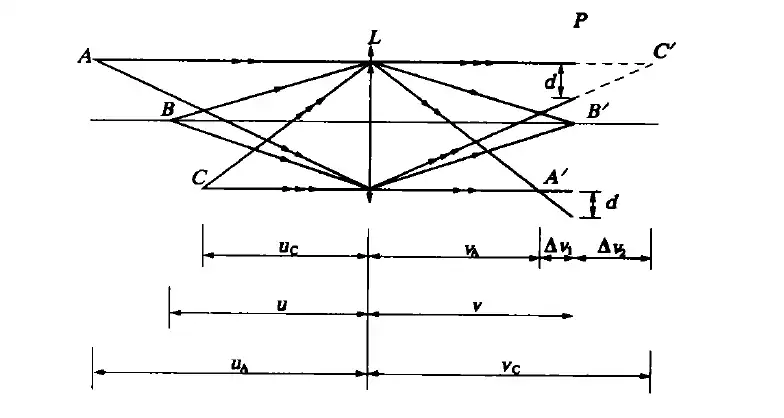
∵uA=u远,vA=v−Δv1,1u+1v=1fdΔv1=DΔvA通光孔直径为D∴Δv1=vdD+d∴1u远=Df+df−udfuD∵F=fD光圈等于焦距除以光孔直径∴u远=f2uf2−(u−f)Fd\begin{align} \because u_A&= u_{\text{远}},v_A=v-\Delta v_1,\frac{1}{u}+\frac{1}{v}=\frac{1}{f} \notag\\\frac{d}{\Delta v_1}&=\frac{D}{\Delta v_A}\quad\text{通光孔直径为D}\notag\\\therefore \Delta v_1&=\frac{vd}{D+d}\notag\\\therefore \frac{1}{u_{\text{远}}}&=\frac{Df+df-ud}{fuD}\notag\\\because F&=\frac{f}{D} \quad\text{光圈等于焦距除以光孔直径}\notag\\\therefore {\color{teal} u_{\text{远}}}&{\color{teal}=\frac{f^2 u}{f^2-(u-f)Fd}} \end{align}∵uAΔv1d∴Δv1∴u远1∵F∴u远=u远,vA=v−Δv1,u1+v1=f1=ΔvAD通光孔直径为D=D+dvd=fuDDf+df−ud=Df光圈等于焦距除以光孔直径=f2−(u−f)Fdf2u
同理可计算得到近景深的公式:
u近=f2uf2+(u−f)Fd\begin{equation}\color{teal}u_{\text{近}}=\frac{f^2 u}{f^2+(u-f)Fd} \end{equation}u近=f2+(u−f)Fdf2u
所以,整体的景深为远景深减去近景深,再记x=u−ff2Fdx=\frac{u-f}{f^2}Fdx=f2u−fFd,则
u近=u1+xu远=u1−x\begin{align} u_{\text{近}}&=\frac{u}{1+x}\\u_{\text{远}}&=\frac{u}{1-x}\end{align}u近u远=1+xu=1−xu
Δu=u远−u近=2ux1−x2\begin{equation}\color{gold} \Delta u = u_{\text{远}}-u_{\text{近}}=\frac{2ux}{1-x^2} \end{equation}Δu=u远−u近=1−x22ux
可以看出景深的大小与摄距、镜头焦距、所用的光圈以及允许的像斑直径都有关系。
影响景深的因素
景深远界限u远u_{\text{远}}u远的最大值为无限大,由式(5)可得xxx的取值范围为x∈(0,1)x\in (0,1)x∈(0,1),由级数的知识可知,当x<1x<1x<1时,11+x\frac{1}{1+x}1+x1的泰勒展开式为:
11+x=1−x+x2−x3+…+(−1)n−1xn+o(xn)\frac{1}{1+x}=1-x+x^2-x^3+…+(-1)^{n-1}x^n+o(x^n)1+x1=1−x+x2−x3+…+(−1)n−1xn+o(xn)
所以景深Δu\Delta uΔu 也可以表示为:
Δu=2ux(1+x2+x4+…+x2(n−1))\begin{equation}\color{gold} \Delta u = 2ux(1+x^2+x^4+…+x^{2(n-1)})\end{equation}Δu=2ux(1+x2+x4+…+x2(n−1))
当使用长焦镜头,大光圈(fff大、FFF大),聚焦距离远大于焦距(u>>fu>> fu>>f)时,x远远小于1,上式中第二项之后则可以省略掉,得到:Δu1=2ux\Delta u_1 = 2uxΔu1=2ux以及x=u−ff2Fd∼uf2Fdx=\frac{u-f}{f^2}Fd\sim\frac{u}{f^2}Fdx=f2u−fFd∼f2uFd ,重新代入可得新的景深公式为:
Δu′=2u2f2Fd\begin{equation}\color{gold} \Delta u^{‘} = \frac{2u^2}{f^2} Fd\end{equation}Δu′=f22u2Fd
理论上来讲,可以根据此公式绘制个图,但是变量有四个——允许斑点直径d可以设为定值,但光圈FFF不是连续的,镜头的焦距fff也经常不是连续的。画的话很麻烦(我太菜)——Δu(u,f,F,d)\Delta u(u,f,F,d)Δu(u,f,F,d)是一个四维不连续立体图,这里就留个坑,日后来补。
先说一下结论:
- x很小时(x<0.3x<0.3x<0.3)
- 景深与光圈系数成正比。光圈大,景深小;光圈小,景深大。
- 景深与摄距的平方成正比。摄距远,景深大;摄距近,景深小。
- 景深与镜头焦距的平方成反比。镜头焦距长,景深小;镜头焦距短,景深大。
- x很大时(x>0.5)
- 很容易得到大景深
因为变量太多,所以规律均是相对而言的,即这四个因素在其中三个因素相同时,另一因素对景深大小的影响规律成立。否则,这些“规律”就不一定成立。
一些技巧
- 小景深效果能使环境虚糊、主体清楚,这是突出主体的有效方法之一。景深越小,这种环境虚糊也就越强烈,主体也就更突出。采用“最大光圈+尽可能缩短的摄距+长焦距镜头”能获取最小景深的效果。
- 使所有的被摄景物在画面上都能较为清晰地再现,则需要尽可能大的景深,景深越大,被摄景物的清晰度也就越高。“最小光圈+短焦距镜头”能获取最大景深效果。
- 使用短焦距镜头,采用大摄距和小光圈拍摄时,后景深将远大于前景深。
跋
这篇文章磨磨蹭蹭写了有快一个月了😂,一开始计划是分镜头、机身、选购、拆解维修四个部分写的,但哪有那么均匀完美的分类,机身除了画幅、操作、外观外几乎没有什么值得写的;选购、拆解维修要等我买了用了坏了后再说;镜头又涉及成像原理,内容繁杂得厉害,一写下去根本停不下来。
文章中缺漏还是比较多的,比如:画幅尺寸的计算没有彻底理清,画幅比例到底是历史沿袭下来的还是某个特殊算法得到的?以及照片(一寸、五寸…)、屏幕(24寸…)、纸张(A4、16开…)的标准如何确定。摄影用光的内容,如曝光、快门、ISO没有涉及。典型镜头的型号、价位也没有提到。
虽然如此不完美,我也不想一直拖来拖去了,今晚发布罢了!仔细想来,本站也从来没有一篇可以称得上完美的符合预期文章,我也一直没有能打破时间线的惯性,总想发布新东西,而不是维护旧东西,尽管前者是浮躁的表现,而后者才是博客该做的工作。
在一个地方呆久了,有的人会逐渐精通,然后精益求精、求精益精,有的人则会热情消散,越来越傻。这篇文章,曾给我带来许多热情,比如看到一老乡写的景深公式。而今热情消散,不能再写了,已经变傻了,而且根本写不到头的,每一个细节可以都有上万字的阐述。这是一个业余爱好者所不能也没有能力深究的东西。
-
金伟. 解读平面镜、凸透镜、凹透镜对光作用的若干个案[J]. 新课程(教研版),2010(11):224-225. ↩︎
-
光学透镜的镜面通常是制成球面状的,从透镜中心到周边有一定的曲率,这种透镜称为球面透镜。非球面透镜的镜面则是从透镜中心到周边曲率作连续变化的。 ↩︎
-
Wikipedia contributors, “Peripheral vision,” Wikipedia, The Free Encyclopedia, https://en.wikipedia.org/w/index.php?title=Peripheral_vision&oldid=1229508226 (accessed July 14, 2024). ↩︎
-
赵小麟,胡晓东.统一不同画幅数码相机镜头视角的表示标准[C] 第三届全国医学摄影图像学术会议.2009 ↩︎
-
实际尺寸可能有差异,参见:“1英寸”不等于1英寸,关于CMOS尺寸的那点事-36氪最近总是有人拿1/1.xx英寸来和一英寸比了,我今天就算算,面积到底差多少!下面我以某1/1.28英寸为例1【单反吧】_百度贴吧 ↩︎
